Surface Simplification Using Quadric Error Metrics

这篇论文是最简单基础的QEM算法，核心就是用二次型来求出坍缩后对整体模型损坏最小的边。

算法流程

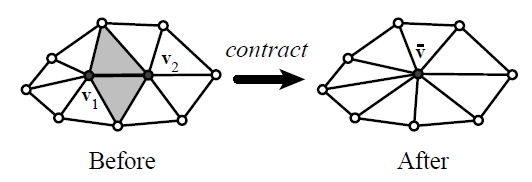
算法主要基于对 vertex pairs 的迭代收缩，如图1所示， $v1,v2$ 是一个 vertex pairs ，消除 $v1,v2$ 生成新的顶点 $\bar{v}$ , 为了在迭代中不断收缩，需要定义收缩的 cost ，每个顶点关联一个实对称矩阵 $Q$ ，对于顶点 $v=[v_xv_yv_z1]$ ,误差 $Δ(v)=v^TQv$ 。对于给定的 vertex pairs 收缩$(v1,v2)→\bar{v}$,使用简易的加法法则 $Q~=Q1+Q2$。

为了执行$(v1,v2)→\bar{v}$ ，需要确定 $\bar{v}$ ，最简单的是选择 $v1,v2$ 或者$ (v1+v2)/2$，这取决于哪个 $\Delta(\bar{v})$最小。不过更好的办法是找到$\bar{v}$ ，因为 $\Delta $是二次的，通过 $δΔ/δx=δΔ/δy=δΔ/δz=0$得到 $\bar{v}$ , $\bar{v}$ 的确定如下所示, 如果 $Δ$ 的行列式为0， $\bar{v}$从 $v1,v2$ 和 $ (v1+v2)/2$ 选择。

二次误差计算

用一个点到以其为顶点的所有面的距离的平方和作为衡量网格变化的误差。设以点 $v$作为定点的面为$ p{1}, p{2}, \ldots p_{k} $, 则点$v $的误差:

$\Delta(v)=\sum_{i=1}^{N}\left(v^{T} p_{i}\right)\left(p_{i}^{T} v\right)=\sum_{i=1}^{N} v^{T}\left(p_{i} p_{i}^{T}\right) v=v^{T}\left(\sum_{i=1}^{N} K_{i}\right) v=v^{T} Q v$

可见, 实际上仅用一个矩阵$ Q $便可刻画一个点与其周围所有面距离的平方和。若在简化过程中, 两个点$ v{1}, v{2} $合成为一个点$v$, 则$ v $的二次误差矩阵$ Q=Q{1}+Q{2} $。为使简化后网格变化最小, 应使简化后点$ v $的二次误差 $\Delta(v)=v^{T} Q v$ 尽可能小。计算可得当$\Delta(v) $极小时,$ v $满足:

$\left[\begin{array}{cccc} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ q_{31} & q_{32} & q_{33} & q_{34} \\ 0 & 0 & 0 & 1 \end{array}\right] v=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]$

这里解出的$ v $即为简化后的点的位置, 而$ Q $为简化后点的二次误差矩阵。

点对的选择

有连边点

若两个点$ v{1} v{2} $之间有相连的边, 则它们组成一个pair, 这个pair可以简化为一个点$ v$, 简化后的二次误差为此次简化的 $cost =v^{T} Q v $ 。为保证最大程度上保留原模型形状，每次应选择cost最小的pair进行简化。

无连边点

对于无连边的点, 当两点之间的距离小于一个给定参数 $ t $ 时, 也将它们视为一个可以简化的pair, 用上述同样的方法计算简化后点的位置、二次误差矩阵, 以及简化cost, 这样的pair也参与到所有pair按照cost的排序中。为了查询与每个点距离小于 $ t $ 的点, 朴素算法是直接遍历求解。但是这样的时间复杂度为 $ O\left(n^{2}\right)$ , 对于一个拥有 $ 10 \mathrm{w} $ 量级顶点的模型来说, 时间成本是不可接受的。因此采用 kdtree 实现 $ \mathrm{t} $ 范围查询, 实现这一步算法的加速。需要注意的是, obj文件坐标大小在 $ 0 \sim 1 $ 之间, 因此当$ t $接近 1 时, 算法退化为遍历求解的情况。不过 $ t $的设置本身是为了合并那些本身距离很近, 但是没有连边的点, 因此一般情况下, $ t $ 很小, 算法加速有效。

KDTree

KDTree是一种分割k维空间的数据结构。每一层比较某一维度。

树的建立

//TreeNode
Node-data - 数据矢量， 数据集中某个数据点，是n维矢量（这里也就是k维）
Range - 空间矢量， 该节点所代表的空间范围
split - 整数， 垂直于分割超平面的方向轴序号
Left - k-d树， 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right - k-d树， 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent - k-d树， 父节点

优化

切分维度优化：构建开始前，对比数据点在各维度的分布情况，数据点在某一维度坐标值的方差越大分布越分散，方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性。
中值选择优化：从原始数据点中随机选择固定数目的点，然后对其进行排序，每次从这些样本点中取中值，来作为分割超平面。该方式在实践中被证明可以取得很好性能及很好的平衡性。

最小堆维护

为实现每次选择cost最小的pair进行合并, 将所有pair按cost组织成一个小顶堆, 支持添加pair (add), 删除堆顶pair(del), 访问堆顶pair(query), 以及更新部分pair(update)。前三种操作均为堆结构的常规操作。需要实现update操作的原因是, 当合并一个pair时, 原来两个点周围的点构成的pair的cost值都将发生变化, 有些将改变其在堆中的位置。
采用lazy维护的方式实现小顶堆的update操作。具体来讲, 将update拆分成remove和add两个操作。add为常规添加操作, remove为在堆任意位置删除操作。 remove堆节点 $ A $ 时, 将其打上lazy标记, 代表其实际已经被删除, 同时在删除堆顶元素的时候, 如果堆顶元素被lazy标记, 则继续删除, 直到没有lazy标记的节点到达堆顶。可以证明, 这样堆中没有lazy标记的节点仍然满足堆序性。

面片反转、重叠问题

一个面三个点的顺序可能会改变，导致面片反转。通过hash定点编号或者计算法向量的方法进行对比可以避免。

Simplifying Surfaces with Color and Texture using Quadric Error Metrics

这篇论文是上一篇的进阶版，主要是把每个顶点的属性加入了权值计算之中，也就是说可以对带材质和其他属性的模型进行简化。

Basic Quadric Error Metric

对于空间中任一平面，方程为 $n^Tv+d=0$ ，其中 $n$ 是法线， $d$ 是一个常量。空间中任意一点 $v$ 到该平面的距离的平方为：

$D^2=(n^Tv+d)^2=v^T(nn^T)v+2dn^Tv+d^2$

这样我们方便定义二次误差 $Q$ :

$Q = (A,b,c)=(nn^T,dn,d^2)$ $Q(v) = v^TAv+2b^Tv+c$

保边

缝隙（原本不相接的部分）

显然在边上找 $\bar{v}$ 会使得权值较小，所以这条边会被保存下来。

假设我们有一个正方体，我们需要缩一条边到一个顶点上。那么在这条边上找顶点就会使得整体的权值损失最小，因为只会影响对侧的两个面。所以其它部分的缝隙会得以保存。

给定的边界

对于和给定的边界相邻的每个面 $p$，都计算一个平面使得这个平面垂直于 $p$，并且穿过与 $p$ 相邻的边。

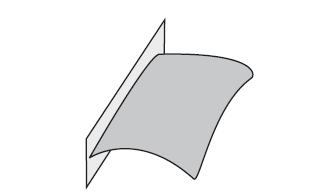
同上所述，这条边界会被保留下来。

带属性的网格简化

考虑三角形 $T=(p,q,r)$，顶点 $p=[p_x,p_y,p_z,p_r,p_g,p_b]^T$。假设三角形内部的点属性可以由三个顶点线性插值得到。三个顶点在 $R^n$ 空间中可以决定一个二维平面。

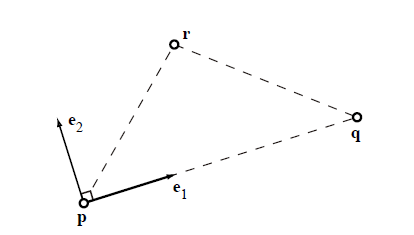
$e_1,e_2$是一组基底向量，可以表示为：

$e_1=\frac{q-p}{||q-p||}$ $e_2 = \frac{r-p-(e_1\cdot{(r-p)})e_1}{||r-p-(e_1\cdot{(r-p)})e_1||}$

对任一点 $v \in R^n$，用 $D^2$表示$v$ 到平面 $T$的距离，令 $u=p-v$，则：

$||u||^2 = ||u\cdot e_1||^2 + ||u\cdot e_2||^2 + ... +||u\cdot e_n||^2$

那这样的话除了前两项，后面的所有$e_i$都和该平面垂直，所以：

$D^2=||u||^2 -||u\cdot e_1||^2 - ||u\cdot e_2||^2$ $D^2 = u^Tu-(u^Te_1)(e_1^Tu)-(u^Te_2)(e_2^Tu)$ $D^2=v^Tv-2p^Tv+p\cdot p\\-v^T(e_1e_1^T)v+2(p\cdot e_1)e_1^Tv-(p\cdot e_1)^2\\-v^T(e_2e_2^T)v+2(p\cdot e_2)e_2^Tv-(p\cdot e_2)^2$

那么我们可以把 $D^2$ 写成上述 $D^2=v^TAv+2b^Tv+c$ 的形式：

$A=I-e_1e_1^T-e_2e_2^T\\b=(p\cdot e_1)e_1+(p\cdot e_2)e_2 -p\\c=p\cdot p-(p\cdot e_1)^2-(p\cdot e_2)^2$

New Quadric Metric for Simplifying Meshes with Appearance Attributes

其实带属性的模型简化方法就是对权值函数加入属性方面的计算。

和上篇的方法不同，不再在 $R^{3+m}$ 的空间中做二次型的最值，而是优化到 $R^3$ 的普通空间中做权值函数的求解。

权值函数被定义为：

$Q^{f}\left(\mathbf{v}=\left(\begin{array}{l} \mathbf{p} \\ \mathbf{s} \end{array}\right)\right)=Q_{p}^{f}(\mathbf{v})+\sum_{j=1}^{m} Q_{s_{j}}^{f}(\mathbf{v})$

其中 $Q{p}^{f}(\mathbf{v})$ 是几何误差，指三维位置上的距离的平方和。$Q{s_{j}}^{f}(\mathbf{v})$ 是属性偏差，指 $s_j$ 属性上的权值偏差。

如之前文章所写：

$Q_{p}^{f}=(\mathbf{A}, \mathbf{b}, c)=\left(\left(\begin{array}{c|c} \mathbf{n n}^{T} & \ddots 0 \ddots \\ \hline \ddots 0 \ddots & \ddots 0 \ddots \end{array}\right),\left(\begin{array}{c} d \mathbf{n} \\ \hline 0 \end{array}\right), d^{2}\right)$

那么对于 $Q_{s_j}^{f}$ ，首先定义一个线性方程：（ $p$ 为一点）

$\hat{s}_{j}(\mathbf{p})=\mathbf{g}_{j}^{T} \mathbf{p}+d_{j}$

对平面 $f=\left(\left(\begin{array}{l}
\mathbf{p}{1} \
\mathbf{s}{1}
\end{array}\right),\left(\begin{array}{l}
\mathbf{p}{2} \
\mathbf{s}{2}
\end{array}\right),\left(\begin{array}{c}
\mathbf{p}{3} \
\mathbf{s}{3}
\end{array}\right)\right)$, $s_j(p)$ 是由线性插值得到的。值得注意的是 $s_j(p) = s_j(p’)$，其中$p’$是点 $p$在$f$上面的投影点。所以有 $n^Tg_j=0$。那么我们的$g_j$和$d_j$可以通过解线性方程得到：

$\left(\begin{array}{ll} \mathbf{p}_{1}^{T} & 1 \\ \mathbf{p}_{2}^{T} & 1 \\ \mathbf{p}_{3}^{T} & 1 \\ \mathbf{n}^{T} & 0 \end{array}\right)\left(\begin{array}{l} \mathbf{g}_{j} \\ d_{j} \end{array}\right)=\left(\begin{array}{c} s_{1, j} \\ s_{2, j} \\ s_{3, j} \\ 0 \end{array}\right)$

这样的话，因为 $Q{s{j}}^{f}(\mathbf{v})=\left(\hat{s}{j}(\mathbf{p})-s{j}\right)^{2}=\left(\mathbf{g}{j}^{T} \mathbf{p}+d{j}-s_{j}\right)^{2}$，所以可以表示成：

$Q_{s_j}^f = (A,b,c)\\=\left(\left(\begin{array}{c|ccc} \mathbf{g}_{j} \mathbf{g}_{j}^{T} & \ddots 0 \ddots & -\mathbf{g}_{j} & \ddots 0 \ddots \\ \hline \ddots 0 \ddots & \ddots 0 \ddots & 0 & \ddots 0 \ddots \\ -\mathbf{g}_{j}^{T} & \cdots 0 \cdots & 1 & \cdots 0 \cdots \\ \ddots 0 \ddots & \ddots 0 \ddots & 0 & \ddots 0 \ddots \end{array}\right),\left(\begin{array}{c} d_{j} \mathbf{g}_{j} \\ \hline 0 \\ -d_{j} \\ 0 \end{array}\right), d_{j}^{2}\right)$

综上所述，整体的权值误差函数就是：

$Q^f=(A,b,c)\\=(\left(\begin{array}{c|c} \mathbf{n n}^{T}+\sum_{j} \mathbf{g}_{j} \mathbf{g}_{j}^{T} & -\mathbf{g}_{1} \cdots-\mathbf{g}_{m} \\ \hline-\mathbf{g}_{1}^{T} & \\ \vdots & I \\ -\mathbf{g}_{m}^{T} & \end{array}\right),\left(\begin{array}{c} d \mathbf{n}+\sum_{j} d_{j} \mathbf{g}_{j} \\ \hline-d_{1} \\ \vdots \\ -d_{m} \end{array}\right), d^{2}+\sum_{j} d_{j}^{2})$

保边

看不懂。

Efficient Minimization of New Quadric Metric for Simplifying Meshes with Appearance Attributes

就讲了一种简化计算的方式。我们有：

$\mathbf{A}=\left(\begin{array}{c|ccc} \mathbf{n n}^{T}+\sum_{j} \mathbf{g}_{j} \mathbf{g}_{j}^{T} & -\mathbf{g}_{1} & \cdots & -\mathbf{g}_{m} \\ \hline-\mathbf{g}_{1}^{T} & & & \\ \vdots & & I \\ -\mathbf{g}_{m}^{T} \end{array}\right), \quad \mathbf{b}=\left(\begin{array}{cc} d \mathbf{n}+\sum_{j} d_{j} \mathbf{g}_{j} \\ \hline-d_{1} \\ \vdots \\ -d_{m} \end{array}\right), \quad c=d^{2}+\sum_{j} d_{j}^{2}$

要计算$Q^f$的最小值，就是要求：

$\bigtriangledown Q^v(v) =2Av + 2b$

即：

$Av_{min} = -b$

$A$ 是一个 $3+m$ 行的矩阵，正常来说，需要 $O(m^2)$的复杂度，但我们可以用一种简单的方法去求解。

先把方程写成：

$\left(\begin{array}{cc} \mathbf{C} & \mathbf{B} \\ \mathbf{B}^{T} & \alpha I \end{array}\right)\left(\begin{array}{c} \mathbf{p}_{\min } \\ \mathbf{s}_{\min } \end{array}\right)=\left(\begin{array}{l} \mathbf{b}_{1} \\ \mathbf{b}_{2} \end{array}\right)$

然后对下面的$m$ 行，每行乘以$-B/\alpha$ ，再把它们加到一开始的三行里。（因为 $C$ 是一个$3×3$的矩阵）

$\left(\mathbf{C}-\frac{1}{\alpha} \mathbf{B B}^{T}\right) \mathbf{p}_{\min }=\mathbf{b}_{1}-\frac{1}{\alpha} \mathbf{B}_{2}$

这就是一个 $3×3$的线性方程求解了，时间固定。然后再

$\mathbf{s}_{\min }=\frac{1}{\alpha}\left(\mathbf{b}_{2}-\mathbf{B}^{T} \mathbf{p}_{\min }\right)$

这样的话整体的求解就降低到了$O(m)$的复杂度。

Mesh Simplify Notes